Проблема применения метода Мартингейла
Иногда в Интернете можно прочитать, что методом Мартингейла не удается выиграть в казино. Посмотрим, какие могут быть причины.
Если идет серия непрерывных проигрышей, то размер ставки нарастает в геометрической прогрессии. Для базового варианта стратегии Мартингейла ставка при каждом проигрыше удваивается. Значит, если в очередной раз Вы не сможете удвоить свою ставку по причине нехватки Ваших денег, то базовая схема Мартингейла будет нарушена.
В этой ситуации Вы поставите ставку меньшую чем нужно. Значит, даже если эта ставка выиграет, то она не компенсирует все предыдущие проигрыши в серии проигрышей. И Ваш капитал не восстановится до такого размера, который у него был перед началом серии проигрышей.
Далее Вы начнете играть с меньшего капитала. Но если Вам попадется снова такая же серия проигрышей, то Вы проиграете Все свои деньги.
Вероятность разорения
Поэтому на первом этапе надо вычислить вероятность появления серии непрерывных проигрышей. Эта задача легко решается. Пусть мы хотим сделать N ставок, а нас интересует, какова вероятность того, что при этом мы встретим серию проигрышей длиной M ставок и более чем M ставок.
Оказывается, эта вероятность равна
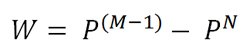
где P, это вероятность выпадения проигрыша на очередной ставке.
Например, для игры в орлянку вероятность выпадения проигрыша на каждой ставке равна 1/2. Значит, эта формула будет
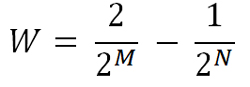
Для базового метода Мартингейла в европейскую рулетку приблизительно P=1-0.486=0.514, а в американскую примерно P=1-0.474=0.526. (Данные взяты из статьи с описанием базового варианта стратегии Мартингейла.)
Нам сейчас важно разобраться в сути, а не в деталях. Поэтому всё дальнейшее рассмотрение мы сделаем не для рулетки, а для игры в орлянку. Для рулетки будет всё то же самое, только цифры другие.
Кроме того, мы будем считать, что общая серия всех ставок N у нас много больше, чем такая минимальная серия ставок M, которая может нас разорить. Поэтому мы пренебрегаем вторым слагаемым в формуле вероятности выпадения серии проигрышей. Формула вероятности выпадения серии из M и более проигрышей для орлянки упрощается и становится такой
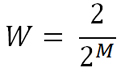
Анализ формулы вероятности выпадения серии непрерывных проигрышей
Из этой формулы видно, что вероятность выпадения одного проигрыша и более (двух, трех, и т.д.) будет равна единице. (На самом деле чуть меньше единицы, если учесть второе отброшенное слагаемое.) Вероятность выпадения двух и более подряд идущих проигрышей будет приблизительно равна 1/2. Вероятность последовательного выпадения трех и и более идущих подряд проигрышей будет равна 1/4. И т.д.
Например, если у нас сейчас на руках всего 7 рублей, а минимальная ставка равна одному рублю, то для разорения достаточно, чтобы прямо сейчас выпала серия из трех и более проигрышей. На первом проигрыше мы теряем один рубль, на втором теряем 2 рубля, на третьем - 4 рубля, и всё, проиграли все 1+2+4=7 рулей. Вероятность встретить сразу сейчас такую серию проигрышей длины 3 или 4 или 5 и т.д. по нашей формуле будет равна 1/4, так как M=3.
Таким образом, если Вы играете в орлянку, используя базовый метод Мартингейла, и у Вас всего 7 рублей, то в такой ситуации в каждом четвертом случае Вас ждет разорение. Это означает, что если 4 игрока начинают сейчас играть в орлянку по классической стратегии Мартингейла и у каждого из них всего 7 рублей, то один игрок сразу разоряется.
Из формулы видно, что вероятность разориться в классическом Мартингейле есть всегда. Если Вам кто-то говорит, что такой вероятности разориться нет, то значит, Вам просто врут.
Как уменьшить вероятность разорения
Однако, есть одна очень-очень приятная вещь. Эта вероятность разорения в классическом Мартингейле очень быстро экспоненциально убывает, при увеличении Вашего капитала.
Например, если у Вас 63 рубля то Вас может разорить серия из 6 проигрышей и более. Ведь число 63 является суммой из шести слагаемых, которые являются степенями двойки, 63=1+2+4+8+16+32. А вероятность выпадения такой серии проигрышей будет уже всего W=1/32=0.03125. Это чуть больше чем 3%. Это означает, что если 100 игроков начинают сейчас играть в орлянку и у каждого всего 63 рубля, то всего лишь только 3 игрока сразу разорятся.
Вывод: Таким образом, чем у Вас больше размер капитала, тем меньше вероятность разорения при использовании основной стратегии Мартингейла. В принципе, можно подобрать такой большой размер капитала, что вероятность разорения будет меньше, чем вероятность того, что завтра Вам на голову упадет кирпич или метеорит.
Если при игре в орлянку по базовой стратегии Мартингейла у игрока 1023 рубля, то его разорит серия из 10 непрерывных проигрышей, так как число 1023, эта сумма из десяти первых степеней двойки, 1023=1+2+4+8+16+32+64+128+256+512. При M=10 вероятность того, что сейчас выпадет серия из 10 и более проигрышей будет примерно W=1/512=0.002. То есть если сейчас начнут с таким капиталом играть 1000 игроков, то сразу разорятся всего лишь только 2 игрока.
Отношение капитала к минимальной ставке
Если быть более точным, то играет роль не столько сам размер Вашего капитала, сколько отношение размера капитала к минимальной ставке, которую Вы ставите после очередного выигрыша.
Например, если у Вас те же самые 1023 рубля, но Вы по какой-то причине ставите не 1 рубль, а 10 рублей (сами так захотели или условия игры такие, что минимальная ставка 10 рублей), то Вы разоритесь на серии проигрышей равной уже не десяти, а только семи, так как 1023=(10+20+40+80+160+320)+393. На первых шести проигрышах Вы проиграете 630 рублей. И у Вас останется только 393 рубля, которые Вы проиграете на следующем седьмом проигрыше. (Для удвоения ставки Вам нужно 640 рублей, а осталось только 397.) Понятно, что вероятность выпадения семи проигрышей подряд будет уже больше, чем вероятность выпадения непрерывной серии из 10 проигрышей.
Таким образом, сумма одна и та же 1023 рубля, а риск при минимальной ставке 10 рублей будет больше, чем при минимальной ставке в один рубль. Чтобы узнать, во сколько раз увеличился риск, надо вероятность разорения для серии из семи непрерывных проигрышей W=1/64 разделить на вероятность разорения для серии из 10 непрерывных проигрышей W=1/512.
Получаем, что риск увеличился в 8 раз при минимальной ставке в 10 рублей, по сравнению с минимальной ставкой в 1 рубль.
Число 8 это степень двойки с показателем степени равным разнице минимальных длин разорительных серий. У нас для минимальной ставки 1 рубль такая серия равна 10, а для минимальной ставки 10 рублей такая серия равна 7. Получаем 10-7=3. Значит, 2 в степени 3 будет 8.
Если бы минимальная ставка была бы не 1 рубль, а, например, 30 рублей, то для разорения нужна серия из 6 непрерывных проигрышей, так как 1023=(30+60+120+240+480)+93. В этом случае риск увеличивается уже в 16 раз, так как 10-6=4, а 2 в степени 4 равно 16.
Рабочая таблица игрока
Эта таблица показывает, как уменьшается вероятность разорения игрока при применении классической стратегии Мартингейла при игре в орлянку и в европейскую рулетку, в зависимости от отношения величины текущего капитала к величине ставки, которую ставят после каждого выигрыша.
| Отношение капитала к базовой ставке | Минимальная серия проигрышей | Орлянка | Европейская рулетка |
| 1 | 1 | 1 | 1 |
| 2 - 3 | 2 | 0.500000 | 0.513514 |
| 4 - 7 | 3 | 0.250000 | 0.263696 |
| 8 - 15 | 4 | 0.125000 | 0.135412 |
| 16 - 31 | 5 | 0.062500 | 0.069536 |
| 32 - 63 | 6 | 0.031250 | 0.035707 |
| 64 - 127 | 7 | 0.015625 | 0.018336 |
| 128 - 257 | 8 | 0.007813 | 0.009416 |
| 256 - 511 | 9 | 0.003906 | 0.004835 |
| 512 - 1023 | 10 | 0.001953 | 0.002483 |
| 1024 - 2047 | 11 | 0.000977 | 0.001275 |
| 2048 - 4097 | 12 | 0.000488 | 0.000655 |
| 4096 - 8191 | 13 | 0.000244 | 0.000336 |
| 8192 - 16383 | 14 | 0.000122 | 0.000173 |
| 16384 - 32767 | 15 | 0.000061 | 0.000089 |
| 32768 - 65535 | 16 | 0.000031 | 0.000046 |
| 65536 - 131071 | 17 | 0.000015 | 0.000023 |
| 131072 - 262143 | 18 | 0.000008 | 0.000012 |
| 262144 - 524287 | 19 | 0.000004 | 0.000006 |
| 524288 - 1048575 | 20 | 0.000002 | 0.000003 |
А это график, который показывает, как экспоненциально быстро убывает вероятность разорения при применении базового варианта стратегии Мартингейла с ростом необходимой серии непрерывных проигрышей.
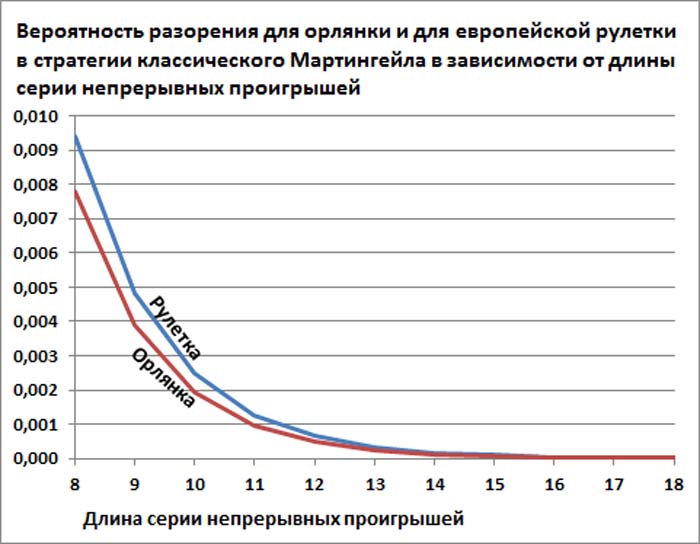
Как видите, по порядку величины вероятности разорений для орлянки и для европейской рулетки примерно совпадают. Вероятность разорения для рулетки всегда чуть больше из-за сектора зеро. (См. описание варианта базового метода Мартингейла для европейской и американской рулеток.)
Теперь посмотрим, как нужно пользоваться этой таблицей.
Практическое применение рабочей таблицы
Допустим, у Вас есть $100. В одном казино Вам предлагают европейскую рулетку с минимальной ставкой $10, а в другом казино Вы можете играть в такую же европейскую рулетку с минимальной ставкой всего 10 центов. В первом случае отношение Вашего капитала к минимальной ставке равно 100/10=10, а во втором случае 100/0.10=1000.
Находим в первом столике таблицы строки с отношением равным 10 и равным 1000. Смотрим, на какой серии непрерывных проигрышей мы можем разориться и какова вероятность встретить эту серию проигрышей.
Для отношения равного 10 получаем, что нас может разорить серия из 4 непрерывных проигрышей и вероятность встретить такую серию будет примерно 0.135. Лично я никогда не буду с такими деньгами играть в таком казино по стратегии базового Мартингейла. Слишком высокая вероятность (больше 10%) встретить серию из 4 непрерывных проигрыша.
Для отношения равного 1000 получаем, что нас может разорить серия из 10 непрерывных проигрышей. При этом вероятность встретить такую серию будет примерно 0.0025. Это всего четверть процента. В эту рулетку можно играть по стратегии классического Мартингейла.
